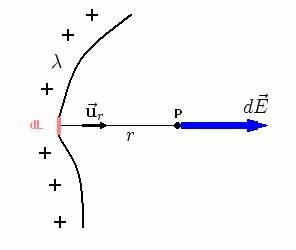
Distribuci�n lineal de carga
Si se dispone de una distribución lineal continua de carga, el campo producido en un punto cualquiera puede calcularse dividiendo la carga en elementos infinitesimales dq. Entonces, se calcula el campo d E que produce cada elemento en el punto en cuestión, tratándolos como si fueran cargas. La magnitud de d E está dada por:
El campo resultante en el punto se encuentra, entonces, sumando; esto es, integrando; las contribuciones debidas a todos los elementos de carga, o sea,

Si la distribución continua de carga que se considera tiene una densidad lineal de carga  , entonces
, entonces  .
.
Por lo tanto,