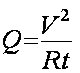Con este recurso se presentará el concepto de circuito eléctrico y se analizarán algunos de sus parámetros, como voltaje, resistencia e intensidad de corriente, relacionándolos mediante la ley de Joule.
Circuitos eléctricos
Efecto o Ley de Joule
Efecto Joule
Este efecto, también conocido como la ley de Joule, es una ley física que expresa la relación entre el calor generado y la corriente que fluye a través de un conductor. Su nombre se debe a James Prescott Joule, quien estudió el fenómeno, y se expresa matemáticamente de la siguiente manera:
Donde Q es el calor generado por una corriente constante fluyendo a través de un conductor con una resistencia eléctrica R, durante un tiempo t. Cuando la corriente, la resistencia y el tiempo se expresan en amperes, ohms y segundos respectivamente, entonces la unidad de Q es el joule. A la primera ley de Joule, en ocasiones se le conoce como la ley de Joule-Lenz, puesto que fue descubierta más tarde y de manera independiente por Henrich Lenz. El efecto de calentamiento de los conductores que transportan corrientes se conoce como calentamiento de Joule; es decir, cuando por un material conductor con resistencia no nula "R" -es decir la práctica totalidad de los materiales conductores- circula una corriente "I" se produce un calentamiento en el material.

En la figura podemos observar una aplicación clásica del efecto de calentamiento de la Ley de Joule: la parrilla eléctrica.
La ley de Joule está íntimamente relacionada con la ley de Ohm. A continuación, mostramos el procedimiento matemático mediante el cual las dos leyes se relacionan:
Primero escribimos la ley de Ohm:
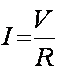
Ahora la potencia disipada en un resistor:
Combinando las dos ecuaciones y poniéndolas en términos de I y R, tenemos:
esta última expresión representa la potencia disipada en un resistor en términos de la corriente (watts o joules/segundo).
Finalmente la cantidad de potencia disipada por un resistor es la cantidad de trabajo hecho sobre el resistor (es decir, el calor disipado en el resistor) dividido por el intervalo de tiempo:
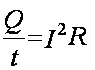
Despejando esta ecuación obtenemos:
Observamos que la ley de Joule también se puede escribir en términos del voltaje a través del resistor: