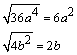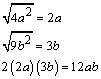El prop�sito de este objeto de aprendizaje es que el alumno realice la factorizaci�n de trinomios cuadrados perfectos; para ello se presentar�n ejemplos y ejercicios propuestos para ser resueltos por el estudiante.
Factorización
Trinomio cuadrado perfecto
Se dice que un trinomio es trinomio cuadrado perfecto (TCP) si tiene la forma:
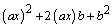
y es el resultado de elevar al cuadrado un binomio de la forma:
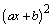
Regla para conocer si un trinomio es cuadrado perfecto:
Un trinomio es cuadrado perfecto cuando el primero y el tercer término son cuadrados perfectos (o tienen raíz cuadrada exacta) y positivos, y el segundo término es el doble producto de las raíces cuadradas de esos términos.
Ejemplo
¿Cuáles de los siguientes trinomios son cuadrados perfectos?
Veamos cual de ellos cumple con las condiciones para que un trinomio sea cuadrado perfecto.
Es un TCP.
La raíz del segundo término no es exacta, entonces no es TCP.
Es un TCP.
Regla para factorizar un trinomio cuadrado perfecto:
Se extrae la raíz cuadrada al primero y el tercer término del trinomio, se forma con ellas un binomio con el signo del segundo término, y el binomio así formulado se eleva al cuadrado.
Ejemplo
Factoriza el siguiente trinomio cuadrado perfecto:
.
Ejercicios
Factoriza los siguientes trinomios como trinomios cuadrados perfectos.
1.
Solución
2.
Solución
3.
Solución
4.
Solución
5.
Solución