Dominio, rango y gr�fica de funciones exponenciales
Debido a que las reglas de asociación de las funciones exponenciales tienen la forma 
Su dominio son todos los números reales
.
Su rango es:
Los reales positivos
si
.
- Los reales negativos
si
.
Es importante decir cuándo una función es creciente y cuándo es decreciente:
Se dice que una función es creciente si, al aumentar el valor de la variable
, aumenta el valor de la función
.
Se dice que una función es decreciente si, al aumentar el valor de la variable
, disminuye el valor de la función
.
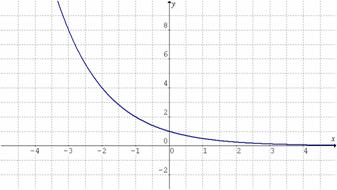
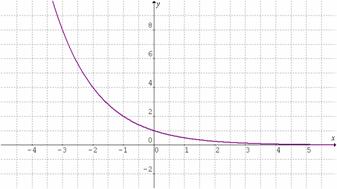
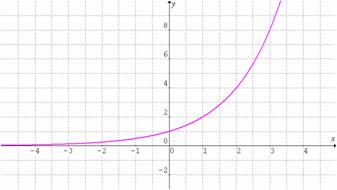
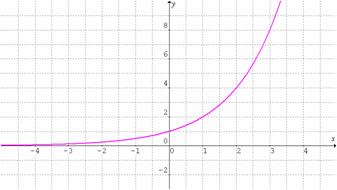
Observemos las gráficas de las funciones exponenciales 
y 
.
 |
|
es una función creciente; su rango son los reales positivos, ya que 
|
|
es una función decreciente; su rango son los reales positivos, ya que 
De aquí podemos concluir que una función exponencial 
con 
es:
-
Creciente si
(
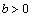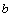es el coeficiente de 
). -
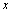Decreciente si
(
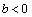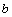es el coeficiente de 
).
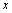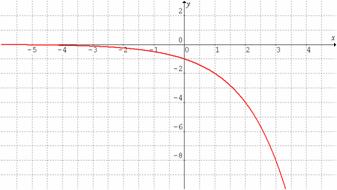
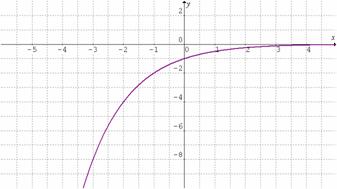
Observemos que si 
las gráficas se “voltean” y el rango cambia, al igual que la condición de ser creciente y decreciente.
|
|
es una función decreciente; 
y su rango son los reales negativos, ya que 
.
|
|
es una función creciente; 
y su rango son los reales negativos, ya que 
.
Resumiendo tenemos que:
|
Rango |
Creciente |
Decreciente |
 |
 |
 |
 |
 |
 |
 |
 |
Ahora vamos a ver qué sucede cuando la base a satisface las condiciones 
o 
.
Tomemos como ejemplo la función |
|
.
.
Tomemos como ejemplo la función |
|
.
.
Con la información proporcionada es posible identificar la gráfica y determinar el dominio y rango de una función exponencial.