Torsión

Deformaciones en un elemento circular

Si consideramos un elemento de sección transversal circular, en su rango elástico, sometido a un par de torsión en uno de los extremos mientras que el otro permanece fijo –como se muestra en la siguiente animación– puede observarse que el extremo sometido al par de fuerzas girará con respecto al extremo izquierdo en un cierto ángulo denominado ángulo de giro o ángulo de torsión (φ).

Se puede observar que cada una de las secciones transversales sufre un giro que está en función de la distancia del extremo fijo. Este ángulo de giro es proporcional a el torque T, pero también varía linealmente con la distancia. Es decir, el ángulo de giro para el extremo fijo es cero, para el extremo libre es φ y para la sección transversal de la barra que se encuentra a la mitad, es φ/2.

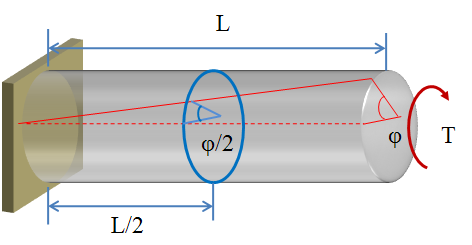
Aprovechando esta linealidad, puede definirse la deformación cortante unitaria que representa la distribución lineal con la que se ha deformado el elemento. Es claro que la deformación máxima ocurre en el extremo libre, y si denotamos a r por el radio del cilindro, la distancia circular que se ha desplazado el extremo libre es φL, pero sabemos que esa distancia también es la deformación unitaria máxima multiplicada por la longitud de la barra. Esto es:

De donde podemos definir a la deformación cortante unitaria máxima como:

Si queremos averiguar la deformación específica que ocurre en una sección interior que está a una distancia radial ρ del eje de la barra:

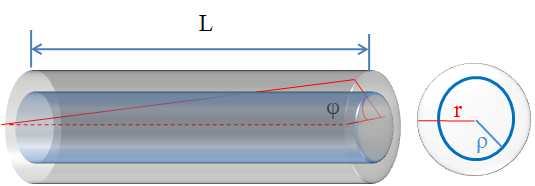
Podemos calcularla como:

Que al sustituir el valor del ángulo de torsión, por su despeje de la ecuación de deformación cortante unitaria máxima, se tiene: