Con este recurso se introducirá al alumno en los conceptos de aceleración media y aceleración instantánea. Se presenta la solución detallada de un problema de aplicación y se solicita resolver otro.
Movimiento rectilíneo
Aceleración media e instantánea
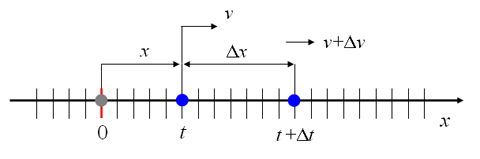
En la sección anterior hemos definido la velocidad instantánea como la derivada de la posición respecto del tiempo. En esta sección analizaremos el concepto de aceleración, la cual se origina cuando la velocidad cambia al transcurrir el tiempo.
|
La aceleración media de un objeto en movimiento se define como el camnio de la velocidad en un intevalo de tiempo.
En donde 
representa un incremento en el tiempo, mientras que 
representa el correspondiente cambio de velocidad. Por otra parte, análogamente a la velocidad instantánea, podemos definir tambien la aceleración instantánea como el siguiente límite:
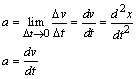
La posición, velocidad y aceleración son vectores, y la notación vectorial ha sido omitida para estas expresiones porque al ser el movimiento rectilíneo se suponen las direcciones como conocidas y las relaciones escritas en líneas anteriores denotan las magnitudes de la velocidad y la aceleración.
Podemos reescribir las ecuaciones de velocidad y aceleración despejando dt de la siguiente manera:
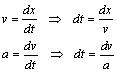
Igualando ambas expresiones se obtiene:
Pasamos el termino v al lado izquierdo de la igualdad y a al lado derecho para encontrar:
en esta expresión se relacionan la aceleración con la posición y la velocidad sin incluir el tiempo.
Resumen
Las ecuaciones generales del movimiento son:
velocidad media
velocidad instantánea
aceleración instantánea
ésta nos relaciona la posición velocidad y aceleración sin importar el tiempo.
A partir de estas se encuentra la expresión matemática que permite describir el movimiento de un cuerpo en un cierto intervalo de tiempo.