Con este objeto de aprendizaje, el alumno aplicará la segunda ley de Newton en la solución de problemas.
Segunda ley de Newton
Segunda ley de Newton ´
Antes del siglo XVII todo el mundo creía que para mantener un objeto en movimiento a velocidad constante hacía falta una fuerza constante. ¿Tú qué opinas?, ¿qué pasa cuando dejas de empujar un carrito de juguete, por ejemplo? Se para de inmediato, ¿no? La experiencia cotidiana, al parecer, confirma la creencia. A principios del siglo XVII Galileo Galilei se puso a hacer experimentos con pelotas y planos inclinados. Soltó una pelota por un plano inclinado desde cierta altura. La pelota bajó y luego subió por otro plano inclinado. Usando bolas y planos muy lisos Galileo observó que las pelotas subían casi hasta el mismo nivel del que habían partido. |

Casi, pero no exactamente. ¿Por qué? Galileo se dijo que el intervalo que les faltaba para llegar hasta el mismo nivel se debía a que algo perdía la pelota en su camino debido a la fricción. Pero si pudiera eliminarse la fricción completamente, ¿qué pasaría? Galileo pensaba que sin fricción las pelotas llegarían exactamente hasta la misma altura de la que partieron.

Si no hubiera fricción las pelotas llegarían exactamente hasta el mismo nivel. ¿Estás de acuerdo?
Entonces a Galileo se le ocurrió la siguiente variación sobre su experimento: hacer bajar gradualmente el plano inclinado por el que sube la pelota después de bajar por el plano inclinado inicial, y lanzar pelotas a cada paso. ¿Hasta dónde sube la pelota cuando el segundo plano inclinado está menos inclinado que el primero?
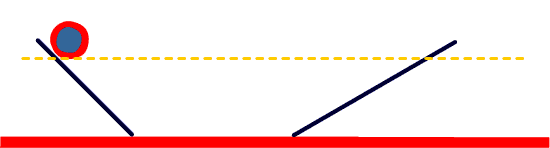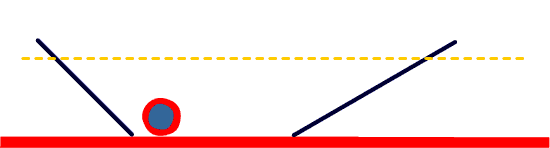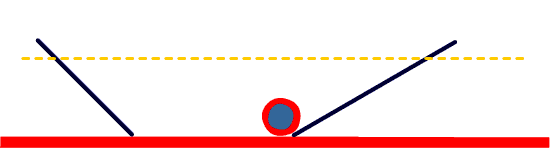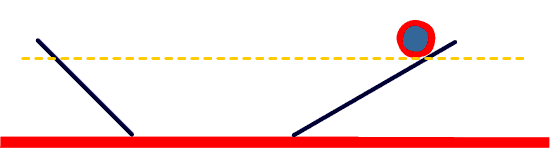

Si el segundo plano inclinado está menos inclinado que el primero, la pelota recorre una distancia mayor en ese plano para llegar hasta el mismo nivel
Luego Galileo se preguntó: ¿y si el segundo plano no está inclinado en absoluto? ¿Hasta dónde llega la pelota?

¿Hasta dónde llega la pelota si el segundo plano no está inclinado? ¿Tratará de llegar hasta el mismo nivel? ¿Qué distancia recorrerá?
Galileo concluyó que, cuando se elimina la fuerza de fricción que hace perder impulso, los objetos en movimiento siguen en movimiento sin necesidad de fuerza.
Para detener un objeto (o para ponerlo en movimiento si está en reposo) se necesita aplicar una fuerza.

¿Cuál de estos dos objetos alcanzará más rápido la velocidad de 1 metro por segundo?

¿Cuál de estos dos objetos alcanzará más rápido la velocidad de 1 metro por segundo?

¿Cuál de estos dos objetos alcanzará más rápido la velocidad de 1 metro por segundo? ¿Hay suficiente información para decidirlo?
Aplicar una fuerza a un objeto produce una aceleración (un aumento o disminución de la velocidad). A mayor fuerza, mayor aceleración. Pero al mismo tiempo, a mayor masa, menor aceleración. Isaac Newton encontró la relación exacta entre intensidad de la fuerza, masa y aceleración:
Relaci�n entre la fuerza, masa y aceleraci�n
Ésta es la versión más sencilla de la segunda ley de Newton. La general es más complicada. Para entenderla necesitas entender primero el concepto de derivada de una función, que se aprende en cálculo diferencial. He aquí, por cierto, que Newton tuvo que inventar primero el cálculo diferencial para poder encontrar la relación entre la fuerza, la masa y la aceleración.
I. Resumen y método
En la sección anterior, concluimos que:
1. Si un cuerpo se encuentra bajo la acción de una fuerza F, entonces la aceleración de este cuerpo es inversamente proporcional a su masa:
2. La aceleración del cuerpo es directamente proporcional a la fuerza que actúa sobre él:
Estos resultados pueden ser representados mediante la siguiente ecuación:
Si de la ecuación anterior se despeja la fuerza F, entonces se obtiene la segunda ley de Newton:
Si sobre un cuerpo actúa más de una fuerza, la segunda ley de Newton puede extenderse para incluir a todas las fuerzas. El resultado es un sistema de ecuaciones:
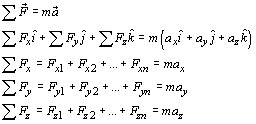
Analicemos el caso en el que un cuerpo está sometido por varias fuerzas, y aplicaremos la segunda ley de Newton para determinar las ecuaciones de movimiento de este cuerpo.
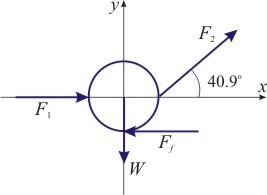
Si trasladamos todas las fuerzas, de tal manera que sean aplicadas en el mismo punto del cuerpo, se obtiene el siguiente diagrama de cuerpo libre (DCL)
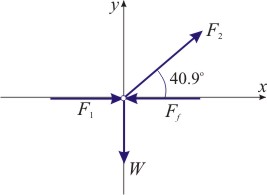
Para realizar el análisis de fuerzas, es necesario descomponer cada fuerza en sus componentes rectangulares (x,y):
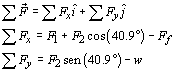
En el curso de estática se vio que la suma de fuerzas debe ser igual a cero cuando el cuerpo está en equilibrio; pero en el curso de cinemática se dijo que la fuerza resultante puede ser diferente de cero y, en consecuencia, el cuerpo se estaría moviendo, por lo que hay que aplicar la segunda ley de Newton para obtener el siguiente sistema de ecuaciones:
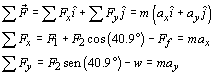
Una vez resolviéndolo, se conocerá la magnitud de cada una de las fuerzas involucradas en el sistema.
Ejemplos de aplicación
Accede a cada uno de los siguientes vínculos, para que conozcas algunas aplicaciones prácticas de los conceptos que has estudiado en esta unidad, así como para que observes la forma en que se resuelven los problemas relacionados.
Ejemplos resueltos y ejercicios propuestos